Журнал «Боль. Суставы. Позвоночник» Том 13, №4, 2023
Вернуться к номеру
Оцінка біологічного віку кісткової системи за допомогою множинної регресії та нейромережевого аналізу
Авторы: N.V. Grygorieva (1), A.V. Pisaruk (1), V.H. Gurianov (2), А.S. Musiіenko (1), V.V. Shatylo (3)
(1) - State Institution “D.F. Chebotarev Institute of Gerontology of the NAMS of Ukraine”, Kyiv, Ukraine
(2) - Bogomolets National Medical University, Kyiv, Ukraine
(3) - National Technical University “Ihor Sikorskyi Kyiv Polytechnic Institute”, Kyiv, Ukraine
Рубрики: Ревматология, Травматология и ортопедия
Разделы: Клинические исследования
Версия для печати
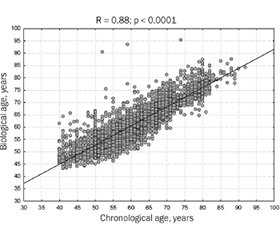
Актуальність. На сьогодні в численних дослідженнях підтверджено зростання ризику остеопорозу в осіб літнього й старечого віку. Стратегії оптимізації діагностики остеопорозу включають комбіноване використання різних методів, тому розрахунок біологічного віку (БВ) кісткової тканини також може бути важливим у прогнозуванні захворювання. Останнім часом запропоновано нові підходи до розрахунку БВ за допомогою математичних методів аналізу, проте дослідження з використанням цих підходів, зокрема нейронної мережі (НМ), в Україні обмежені. Метою дослідження була розробка моделі БВ кісткової тканини та порівняння її точності за допомогою методів покрокової множинної регресії (ПМР) і НМ-аналізу. Матеріали та методи. В одноцентровому когортному дослідженні ретроспективно проаналізовано показники 3071 здорової жінки віком 40–90 років. Аналіз включав антропометричні параметри, показники двохенергетичної рентгенівської абсорбціометрії та 10-річної ймовірності основних остеопоротичних переломів (FRAX). Для розробки моделей БВ кісткової тканини використовували метод ПМР, а побудову моделі НМ проводили за допомогою моделі багатошарового персептрона. Результати. У результаті розрахунку отримано формулу ПМР для БВ кісткової тканини, що включає показники мінеральної щільності кісткової тканини (МЩКТ) поперекового відділу хребта, променевої кістки, мінімальні показники МЩКТ проксимального відділу стегнової кістки, трабекулярний кістковий індекс та FRAX. Рівняння ПМР дозволило розрахувати БВ кісткової тканини з похибкою менше 4,9 року для досліджуваної та контрольної груп і продемонструвало високий зв’язок між розрахованим БВ та хронологічним віком: R = 0,77; p < 0,00001. Результати НМ-аналізу були найкращими при використанні 6 вхідних змінних та одного внутрішнього шару із 7 нейронів. Зв’язок між біологічним та хронологічним віком був сильним (R = 0,88; p < 0,000001), із середньою похибкою розрахунку віку менше 3,7 року для досліджуваної та контрольної груп. Висновки. Порівняння точності обох моделей при оцінці БВ кістки виявило значну перевагу НМ глибокого навчання, проте навчена модель НМ вимагає спеціалізованого програмного забезпечення, тоді як формулу ПМР можна використовувати без додаткових витрат.
Background. Nowadays, many studies confirm the increased risk of osteoporosis in the elderly. Strategies for optimizing diagnosis include a combined use of various methods, so calculating bone biological age (BA) can also be important for disease prediction. Recently, some new methodological approaches to BA calculation with the mathematical methods implementation were proposed. However, studies utilizing advanced approaches, particularly neural network (NN) in Ukraine, are limited. The purpose of this study was to develop a bone BA model and compare its accuracy using stepwise multiple regression (MLR) and NN analysis methods. Materials and methods. In a single-center cohort study, we retrospectively analyzed the data of 3,071 healthy women aged 40–90 years. The analysis of the study indices included the anthropometric parameters, dual-energy X-ray absorptiometry indices (DXA), and the parameters of the 10-year probability of major osteoporotic fractures (FRAX). For the development of bone BA models, MLR methods were used and the construction of the NN model was performed using a multilayer perceptron model. Results. As a result of the calculation, we received the MLR formula for bone BA determining bone mineral density (BMD) of lumbar spine and radius, minimal femoral and hip BMD as well as Trabecular Bone Score, and FRAX. The MLR equation allowed to calculation of the bone BA with an error of less than 4.9 years for study and control groups and demonstrated the high connection between calculated and chronological (ChrA) ages (R = 0.77; p < 0.00001). The use of NN analysis showed the best results using 6 input variables and 1 internal layer of 7 neurons. The assessment of the connection between BA and ChrA demonstrated a high coefficient of correlation (R = 0.88; p < 0.000001) with an average error of age calculation of less than 3.7 years for the study and control groups. Conclusions. A comparison of the accuracy of both models in bone BA estimation revealed a significant advantage of the deep learning NN, however, the use trained NN model requires specialized software, whereas the MLR formula can be used without additional costs.
біологічний вік; кістка; остеопороз; нейронна мережа; машинне навчання
biological age; bone; osteoporosis; neural network; machine learning
Для ознакомления с полным содержанием статьи необходимо оформить подписку на журнал.
- Ageing-and-health. WHO, 1 October 2022. Available from: https://www.who.int/news-room/fact-sheets/detail/ageing-and-health.
- Ukraine: the “oldest” humanitarian crisis in the world. AGE Platform Europe. Available from: https://www.age-platform.eu/ukraine-the-oldest-humanitarian-crisis-in-the-world.
- Akkawi I., Zmerly H. Osteoporosis: Current Concepts. Joints. 2018 Jun 14. 6(2). 122-127. doi: 10.1055/s-0038-1660790.
- Kanis J.A., Norton N., Harvey N.C. et al. SCOPE 2021: a new scorecard for osteoporosis in Europe. Arch. Osteoporos. 2021 Jun 2. 16(1). 82. doi: 10.1007/s11657-020-00871-9.8.
- Grygorieva N., Kovalenko V., Коrzh М. et al. Guideline for diagnostic, prevention and treatment of postmenopausal osteoporosis. Pain. Joints. Spine. 2023. 13(3). 128-154. doi: 10.22141/pjs.13.3.2023.378.
- ISDC. 2019 ISCD Official Positions. Adults. Avai–lable from: https://iscd.org/learn/official-positions/adult-positions.
- Povorozniuk V., Dzerovych N., Hans D. Trabecular bone score in clinical practice (review). Orthopaedics, Traumatology and Prosthetics. 2015. 2. 126-136. doi: 10.15674/0030-598720152126-136.
- Kaloudis E.-Th. Trabecular bone score for the evaluation of fracture risk: A literature review. JRPMS. 2022. 6(4). 121-127. doi: 10.22540/JRPMS-06-121.
- Kanis J.A., Johansson H., Harvey N.C., McCloskey E.V. A brief history of FRAX. Arch. Osteoporos. 2018 Oct 31. 13(1). 118. doi: 10.1007/s11657-018-0510-0.
- Povoroznyuk V., Grуgorieva N., Kanis J., McCloskey E., Johansson H. Ukrainian Version of FRAX: from creation to validation. Pain. Joints. Spine. 2021. 3. 5-14. doi: 10.22141/2224-1507.3.23.2016.85000.
- McCloskey E.V., Odén A., Harvey N.C. et al. A Meta-Analysis of Trabecular Bone Score in Fracture Risk Prediction and Its Relationship to FRAX. J. Bone Miner. Res. 2016. 31(5). 940-8. doi: 10.1002/jbmr.2734.
- Chan H.P., Hadjiiski L.M., Samala R.K. Computer-aided diagnosis in the era of deep learning. Med. Phys. 2020. 47. e218-27. doi: 10.1002/mp.13764.
- Voitenko V.P., Tokar A.V., Polyukhov A.M. The method of determining the biological age of a person. Ge–rontology and Geriatrics. 1984 Yearbook. Biological Age. Heredity and Aging. Kyiv; 1984. 133-137 (in Ukrainian).
- Park C., Took C.C., Seong J.K. Machine learning in biomedical engineering. Biomed. Eng. Lett. 2018. 8. 1-3. doi: 10.1007/s13534-018-0058-3.
- Colloca G., Di Capua B., Bellieni A. et al. Biological and Functional Biomarkers of Aging: Definition, Cha–racteristics, and How They Can Impact Everyday Cancer Treatment. Curr. Oncol. Rep. 2020. 22. 115. doi: 10.1007/s11912-020-00977-w.
- Xia X., Chen W., McDermott J., Han J.J. Molecular and phenotypic biomarkers of aging. F1000Res. 2017 Jun 9. 6. 860. doi: 10.12688/f1000research.10692.1.
- Hartmann A., Hartmann C., Secci R., Hermann A., Fuellen G., Walter M. Ranking Biomarkers of Aging by Citation Profiling and Effort Scoring. Front. Genet. 2021. 12. 686320. doi: 10.3389/fgene.2021.686320.
- Bao H., Cao J. et al., Aging Biomarker Consortium. Biomarkers of aging. Sci. China Life Sci. 2023. 66. 893-1066. doi: 10.1007/s11427-023-2305-0.
- Jia L., Zhang W., Chen X. Common methods of biological age estimation. Clin. Interv. Aging. 2017. 12. 759-72. doi: 10/2147/CIA/S134921.
- Krøll J., Saxtrup O. On the use of regression analysis for the estimation of human biological age. Biogerontology. 2000. 1. 363-68. doi: 10.1023/A:1026594602252.
- Caballero F.F., Soulis G., Engchuan W., Sánchez-Niubó A., Arndt H. et al. Advanced analytical metho–dologies for measuring healthy ageing and its determinants, using factor analysis and machine learning techniques: the ATHLOS project. Sci. Rep. 2017 Mar 10. 7. 43955. doi: 10.1038/srep43955.
- Wani I.M., Arora S. Deep Neural Networks for Diagnosis of Osteoporosis: A Review. In: Singh P., Kar A., Singh Y., Kolekar M., Tanwar S. (eds) Proceedings of ICRIC 2019. Lecture Notes in Electrical Engineering. 2020. 597. Springer, Cham. doi: 10.1007/978-3-030-29407-6_6.
- Dzierżak R., Omiotek Z. Application of Deep Convolutional Neural Networks in the Diagnosis of Osteoporosis. Sensors. 2022. 22(21). 8189. doi: 10.3390/s22218189.
- Adams J.W., Zhang Z., Noetscher G.M., Nazarian A., Makarov S.N. Application of a Neural Network Classifier to Radiofrequency-Based Osteopenia/Osteoporosis Screening. IEEE J. Transl. Eng. Health Med. 2021 Aug 30. 9. 4900907. doi: 10.1109/JTEHM.2021.3108575.
- Xinghu Yu, Chao Ye, Liangbi Xiang. Application of artificial neural network in the diagnostic system of osteoporosis. Neurocomputing. 2016. 214. 376-381. doi: 10.1016/j.neucom.2016.06.023.
- Tassoker M., Öziç M.Ü., Yuce F. Comparison of five convolutional neural networks for predicting osteoporosis based on mandibular cortical index on panoramic radiographs. Dentomaxillofac. Radiol. 2022 Sep 1. 51(6). 20220108. doi: 10.1259/dmfr.20220108.
- Povoroznyuk V.V. Diseases of the musculoskeletal system in people of different ages (selected lectures, reviews, articles). In 3 volumes. Kyiv; 2009. 664 p. (in Ukrainian).
- Povoroznyuk V.V., Orlyk T.V. Biological age of postmenopausal women with low bone mineral density and vertebral pain syndrome. Herald of Scientific Research. 2015. 1. 38-41 (in Ukrainian). Available from: http://nbuv.gov.ua/UJRN/vndt_2015_1_12.
- Grygorieva N., Dubetska H., Koshel N., Pisaruk A., Antoniuk-Shcheglovа I. Mathematical model of the bone biological age based on the bone mineral density and qua–lity indices and Ukrainian FRAX model. Pain. Joints. Spine. 2022. 12(1). 16-22. doi: 10.22141/pjs.12.1.2022.324.